
01. 재귀함수
- 메서드 본인이 본인을 호출하도록 하는 함수
1) 팩토리얼 구하기
- 5! = 5 * 4 * 3 * 2 * 1
= 120
* 반복문을 통한 구현
public class Factorial1
{
public static void main(String[] args)
{
// 팩토리얼을 구하기 위한 메서드 호출
long result = getFactorial(5);
// 결과 출력
System.out.println(result);
}
public static long getFactorial(int max)
{
long result = 1;
for (int i = max; i > 0; i--)
{
result *= i;
}
return result;
}
}
// 실행결과
1202) 재귀호출을 통한 구현
- 재귀호출은 종료 조건을 명시하지 않으면 무한루프에 빠짐.
재귀호출을 구현할때 가장 먼저 해야 하는 것은 종료조건을 명시하는것.
// 곱셈에서 1은 무의미 하므로
// 조건값이 1보다 작거나 같으면 1을 리턴
if (max <= 1) {
return 1;
}- 팩토리얼을 분석하면 아래와 같이 정의할 수 있다
f(x) = x\*f(x+1) 단, x가 1이하인 경우는 1
public class Factorial2
{
public static void main(String[] args)
{
// 팩토리얼을 구하기 위한 메서드 호출
long result = getFactorial(5);
// 결과 출력
System.out.println(result);
}
public static long getFactorial(int max)
{
if (max <= 1)
{
return 1;
}
return max * getFactorial(max-1);
}
}
// 실행결과
12002. 총 합 구하기
1) 양의 정수 n을 입력받아 1부터 n까지의 총 합을 구하는 기능을 재귀합수로 구현
- n부터 1씩 감소하면서 합산을 하고 1이 되는 순간 종료.
예를 들어 n이 5일 때, 5 + 4 + 3 + 2 + 1이 되어야 한다.
이를 표현하면 다음과 같다.
f(1) = 1
f(n) = n + f(n-1)- 이 수식을 프로그램으로 구현한 결과는 아래와 같다.
import java.util.Scanner;
public class MySum {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.print("양의 정수를 입력하세요: ");
int n = sc.nextInt();
int s = sum(n);
System.out.println("결과값: " + s);
}
public static int sum(int n) {
if (n == 1) {
System.out.println(n);
return 1;
}
System.out.print(n + " + ");
return n + sum(n-1);
}
}
// 실행결과
D:\>java MySum
양의 정수를 입력하세요: 5
5 + 4 + 3 + 2 + 1
결과값: 15
D:\>java MySum
양의 정수를 입력하세요: 7
7 + 6 + 5 + 4 + 3 + 2 + 1
결과값: 28
D:\>java MySum
양의 정수를 입력하세요: 10
10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
결과값: 5503. 구구단
- 구구단을 재귀함수로 출력
public class Gugu
{
public static void main(String[] args)
{
printGugu(7, 1);
}
public static void printGugu(int level, int depth)
{
if (depth > 9)
{
return;
}
System.out.printf("%d x %d = %d\n", level, depth, level*depth);
printGugu(level, depth+1);
}
}
// 실행결과
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 6304. 피보나치 수열
-
피보나치 수는 다음와 같은 초기값 및 점화식으로 정의되는 수열.
F(0)=0
F(1)=1
F(n)=F(n-1)+F(n-2)
- 아래는 피보나치 수열을 그림으로 표현
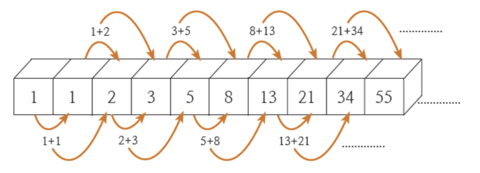
1) 코드로 표현
public class Fibo {
public static void main(String[] args) {
// 0부터 8까지의 피보나치 수 모두 출력
for (int i=0; i<9; i++) {
System.out.printf("%d\t", fibo(i));
}
}
public static int fibo(int n) {
// 전달받은 값과 동일한 값을 리턴한다면 계산할 필요가 없으므로 중단
if (n <= 1) {
return n;
} else {
return fibo(n-2) + fibo(n-1);
}
}
}
// 실행결과
0 1 1 2 3 5 8 13 21'JAVA' 카테고리의 다른 글
| JAVA(자바빈즈(Java Beans), 은닉성, 상속성) (0) | 2020.06.09 |
|---|---|
| JAVA(클래스, 객체, 생성자) (0) | 2020.06.04 |
| JAVA(값 복사 / 참조 복사) (0) | 2020.06.03 |
| JAVA(메서드) (0) | 2020.06.03 |
| JAVA(2차 배열) (0) | 2020.06.02 |




댓글